Geotechnical centrifuge development can correct soil mechanics errors.

This paper makes three points.

The paper will quote Terzaghi, from the Proceedings of the Harvard Conference of the International Society of Soil Mechanics and Foundation Engineering (ISSMFE), June 22 to 26, 1936. The first quotations are from his recollections that he learned to mistrust theory

"some eighteen years ago ..(i.e. in 1918, when).. I went through all the volumes of the leading English, German, and French engineering periodicals which had been published since 1850 and through all the textbooks which I could secure, abstracting all the articles and chapters relating to the subject of my investigations... (When) the theories originated, their authors were still keenly aware of the bold approximations involved, and nobody thought of accepting them at their face value. As the years passed by, these theories were incorporated into the stock of knowledge to be imparted to students during the years of their college training, whereupon they assumed the character of a gospel. Once a theory appears on the question sheet of a college examination, it turns into something to be feared and believed, and many of the engineers who were benefited by a college education applied the theories without even suspecting the narrow limits of their validity. If the structures designed on the basis of these sacred theories stood up, their behaviour was considered normal and not worth mentioning. If they failed it was an act of God, which should be concealed from the eyes of mortals, who might believe the designer was poorly grounded in theory."

The Harvard Proceedings must be read in full to get a full sense of the mixture of enthusiasm and scepticism with which Terzaghi launched his Society. He missed some opportunities for the correction of errors in Harvard, which this paper will discuss.

Terzaghi (1936) placed importance on observations by engineers during construction, of the Panama Canal, or in the construction camps of the US Bureau of Reclamation. "(In) the perpetual war of the civil engineer against the treacherous forces of nature concealed in the earth … scattered and world-wide efforts extending over a period of 25 years (have forged) new and efficient weapons and the prime purpose of our meeting consists in discussing the means of exploiting the advantages thus secured, … (The) possibilities for successful mathematical treatment of problems involving soils are very limited. (The) accuracy of computed results never exceeds that of a crude estimate, and the principal function of theory consists in teaching us what and how to observe in the field. (Successful) work in soil mechanics and foundation engineering requires not only a thorough grounding in theory combined with an open eye for the possible sources of error, but also an amount of observation and measurement in the field far in excess of anything attempted by the preceding generations of engineers. Hence the centre of gravity of research has shifted from the study and the laboratory into the construction camp where it will remain".

The ISSMFE also published a centrifuge paper by Pokrovsky (1936). It is appended below. Terzaghi strongly criticised all papers on small scale physical modelling as "papers whose authors do not hesitate to generalise the conclusions derived from pure theory or from small scale tests on materials with very little if any resemblance to real soils". He stated that "One of the principal goals of instruction in soil mechanics should be to discourage this prevailing tendency to unwarranted generalisation." He went on to speak of "the utter futility of the attempts to discover any single-valued relation between the results of small-scale loading tests and of the settlement of large foundations on stratified soils".

It was an error for Terzaghi to dismiss Povrovsky’s centrifuge technique. The problems that engineers face are so complex that they should exploit any sound technique. Centrifuge tests now solve problems where observation at full scale is no help. One example offshore, where "measurement in the field" is extensively used, has been overturning failure of a jackup rig in storm loading, studied in a centrifuge at small scale, in reduced time, at low cost, not at full scale. Other conditions which can and should be studied in small scale tests include, tidal flood, river flood, earthquake, and prolonged contaminant migration. A model test of a violent event has no publicly unacceptable environmental impact or risk.

The most serious consequence of this error came during the Cold War, after the full scale Nuclear Test Ban, when the US and NATO Allies missed an opportunity to study nuclear weapons effects in centrifuge models. Pokrovsky’s centrifuge paper opens with a statement that in 1936 the laboratory for Physics of the Military-Engineering Academy of the USSR used a centrifuge. Some of us who were engaged in centrifuge modelling 37 years later were at the 1973 Moscow Conference. At that time we thought there had been difficulties by which Pokrovsky’s techniques proved to be less useful than he hoped in 1936. Our Soviet hosts invited all who were interested in centrifuge techniques to a meeting for open discussion with Pokrovsky and other Soviet engineers, at the Hydroproject, after the Conference. In our visit we saw the powerful Hydroproject centrifuge. I was surprised to see in a book by Pokrovsky that the Soviets had successfully modelled nuclear weapons craters. I was told that they wanted the West to become more fully aware of Pokrovsky’s work.

I raised this in subsequent lectures in the USA. The US Defence Nuclear Agency later sponsored crater tests in the Boeing Company centrifuge in Seattle, which led to an order of magnitude reduction of crater size prediction at nuclear explosive levels. In his paper for the San Fransisco TC2 published volume, Schmidt (1988) wrote;

"Results of recent geotechnical centrifuge experiments have dramatically reduced the size estimates for craters formed by near-surface large yield nuclear explosions and by planetary impact of large bodies. Since neither phenomenon can be tested at full scale, centrifuge simulation is the only alternative for obtaining an experimental data base. Estimates of crater size were reduced due to the identification of a strength-gravity transition size, above which cratering efficiency decreases with size. Existing field data were too sparse and were conducted in far too diverse media to observe this pattern. The geotechnical centrifuge has been a valuable experimental technique for investigating explosive and impact cratering behaviour. (The tests) establish the practicality of performing dynamic experiments on the centrifuge, as well as providing a theoretical basis for their interpretation."

Terzaghi’s words on the "utter futility" of small scale tests had made it unlikely that the Allies would, by model tests, find or correct errors after full scale tests were banned; it appears that some Allied weapons would have been dramatically ineffective if Cold War had become War. In contrast, Pokrovsky’s "efforts" gave the Soviets a "new and efficient" research asset. After his early centrifuge model experience he worked on weapons effects during and after World War II. As an expert on cratering he was part of a Soviet elite, (he had the rank of Red Army General and Stalin came to parties where Pokrovsky played the piano at home).

All this was missed in Harvard, yet it is clear in Pokrovsky (1936) that small scale tests did work. No "conclusions derived from pure theory or from small scale tests on materials with very little if any resemblance to real soils" and no "tendency to unwarranted generalisation" are evident in that paper, or in Volume I of Centrifuge 98, which has 147 such papers to consider. No comment that "their authors do not hesitate to generalise" is warranted now, 62 years after the Harvard Conference, and it was not warranted then. At the ISSMFE Tokyo Conference in 1977, when Soviet participants said that the centrifuge was mainly of military significance, I replied that centrifuge techniques were well based in experimental mechanics. Critical state soil mechanics showed reconstituted soil paste to be an effectively stressed elasto-plastic inviscid material in which time effects are due to consolidation. The Soviet analysis in terms of total stress and viscosity made work with Soviet engineers difficult.

In contrast, within the ISSMFE there is acceptance of Terzaghi’s effective stress principle, and the technical committee TC2 has allowed an easy international exchange of information between more than 30 centrifuge centres. Terzaghi’s enquiring spirit, seen in Harvard, lets us question his rejection of "small-scale loading tests". A shear test at very small scale (say on 0.1 to 1 litres of soil) defines soil properties, and a laboratory small scale loading test (say on 100 to 1000 litres of soil) give data of behaviour of soil under gradients of effective stress and pore water pressure. These two sets of test data are sufficient to provide a thorough test of theories, in the "study and the laboratory". This method was used in a US National Science Foundation project on verification of liquefaction analyses, Arulanandin and Scott (1994).

TC2 co-operation mainly concerns construction works and models made of disturbed soil. My own early experience was with well compacted selected fill. Ideas set out in Schofield and Wroth (1968) continued to evolve as I taught and as I saw ground behaviour mechanisms in models made of reconstituted soil. For much construction, I think that soil tests could find the critical state properties of soil selected for a fill, or of soil at a selected site. Designs could aim for ductility, not over compaction. Construction budgets could include the cost of tests to failure of centrifuge models, and observational methods could be based on such tests. Engineers can turn to centrifuge studies, particularly if ground is disturbed or improved, for validation of numerical analyses. 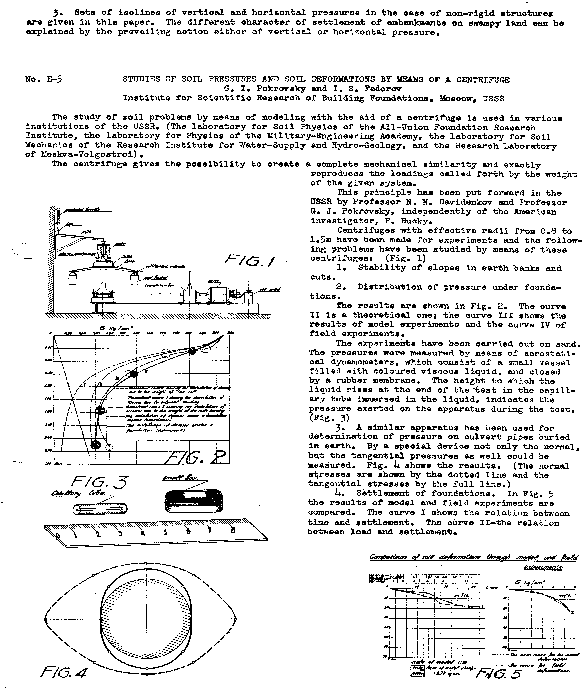There is a choice of alternative centrifuges.

Pokrovsky (1936) Fig. 1 shows a 30g centrifuge made from parts of a Ford truck. One half-shaft stands vertically upright above the differential. The centrifuge rotor replaces a back wheel. The rotor arms slope at 1/30. They act as tension members. In that sense this is not a "beam" centrifuge. The model containers swing up about hinges. They are shown end on. In his test a load bears on a plate, and pressures are measured below the ground surface. In Fig. 2 vertical pressure is plotted against depth with five lines showing pressure as follows;

in ground with self weight, and

1. in an elastic half space under vertical load, and
2. the sum of these two previous pressures, and
3. pressures measured in Pokrovsky’s centrifuge model test, which agree with
4. pressures observed in a full scale test.

Pokrovsky draws a pressure gauge in his Fig. 3. A short length of broken capillary tube was pressed into a small tin full of pink petroleum jelly. The air filled space inside the tube was closed by pink jelly at each end. A rubber membrane covered the jelly. The tin was buried in the model. The model was subjected to high acceleration. The burette was opened. Fluid flowed down along the axis and out to a vessel which applied the required bearing load. After a test the tin was removed and the capillary tube was examined. The pressure increment had compressed the air. Jelly had moved into the ends of the tube leaving a pink stain. Pokrovsky determined the maximum pressure, at that depth, from the minimum length of the air bubble. Both in the full scale test and in the model test he measured pressures up to 50 percent higher than he had calculated theoretically. He had proved that his technique worked, and it was applied to a series of problems where there were no reliable theoretical calculations.

Malushitsky (1975) described the application of Pokrovsky’s technique to problems of mine waste embankments. It gave him a capability for analogue modelling of a problem which he could not solve numerically, with the facilities available to him. His centrifuge could achieve 320g but typical tests were at below 200g. The inside dimensions of his model were length 1400mm, width 500mm, height 750mm, corresponding at 320g to a prototype volume of 17.2 million cubic metres. He built up models in successive layers of reconstituted waste material which he consolidated in flight for long periods. He tested his models by rapid increase of acceleration until there was a slope failure. Academics in the USSR at that time analysed soil as a viscous material under total stress. The scale of time was expected to be the model scale to some power between 0 and 2. Malushitsky found a value of this factor that was appropriate to his class of problem by the technique of modelling the model. His simple instrumentation and the variability between successive models meant that his work took many years. He tested 255 models in total, and writes that they resulted in elimination of landslides at the waste heaps of an open-cast sulphur mine, reduction in re-excavation in internal dumps in an open cast coal mine, and safe tipping of new dry waste on old hydraulic lagoon disposal areas, with savings to industry of about three quarters of a million roubles per year.

The cost of such a facility includes both a beam centrifuge and a strong chamber to enclose it safely, with several model containers for successive tests. Each model is made as a different batch of soil. Several weeks are needed for consolidation of a large model. If models are consolidated on the laboratory floor with a downward hydraulic gradient in order not to tie up the centrifuge, more containers are needed. A model has an unwanted load and unload cycle each time a centrifuge starts and stops, for example to adjust some instrument. Some beam centrifuges now have a facility to manipulate tools in the model container while it is in flight, Derkx, Merliot, Garnier, and Cottineau (1998). Such manipulators are costly because they operate in the high acceleration field of the model test.

I developed drum centrifuges in Cambridge to reduce the cost of centrifuge tests, to improve the accuracy, and reduce the labour and the time needed for any one test series. In order to introduce drum centrifuges safely to other laboratories, I sought a long term commitment from an established manufacturer; financial problems have affected many geotechnical centrifuge developments; their risk was significant and they needed protection of any initial investment. Cambridge University has an intellectual property development plan. After negotiation, a centrifuge manufacturer in the UK, Thomas Broadbent & Sons Ltd. was granted an exclusive licence to incorporate the new intellectual property US Patent 5,634,876 in their "Geotech" centrifuges. One of these came into in operation in Australia, Stewart, Boyle, and Randolph (1998); the next three in Japan; and a fifth is to operate in Switzerland. It is safe to stand by these machines. There is no need to build a reinforced concrete chamber. The centrifuge channel that applies the acceleration to the model layer also contains the soil safely.

In a 2.2m diameter drum centrifuge a channel 0.8m high with 0.2m depth filled with soil forms a single model of large volume and surface. In flight at 320g it is a model of a test site about 2000m long, 256m wide and 64m deep, with a prototype volume of 32.8 million cubic metres. On one model of a uniformly stratified layer of soil, in a 50 footing test series taking 5 weeks, about 20 litres of soil would be closely affected by each test, which is a prototype volume of 655360 cubic metres. A series of similar beam centrifuge tests conducted on models of 80 litres volume at 80g might take ten times longer, and the prototype volume of 40960 cubic metres is sixteen times less. In such tests the walls of the model container would be twice as close to the model test site in the beam centrifuge test series as in the drum series.

The machines are designed for continuous safe operation. Model preparation in the channel, and setting up the test procedure, takes time, but if the test process is automated the channel can then be in continuous flight for several weeks. To change tools which are manipulated and work over the model in flight, a safety shield is lowered to isolate the central plate that supports tools. After this work support is brought to rest, tools can be changed; when it is bought back to channel speed and the shield is raised new tools can work over a chosen test site. Stewart, Boyle, and Randolph (1998) describe both an automated testing system and a data acquisition system. Similar rugged and compact systems provided to the US Army Centrifuge, Waterways Experimental Station, Vicksburg, Miss., and to Toyo Construction Technical Research Institute, Hyogo, Japan, by Carrak (1998), acquire digital data at 5000 samples per second in memory in a logger unit close to the model in the high g field, for uploading to a PC at the control desk. Drum and beam centrifuges operate side by side in centrifuge centres in the UK, Japan, and Australia and complement each other. Any manipulator used in a drum centrifuge can be controlled from the centre of the drum at low g. When both beam and drum centrifuges are used on a single project, test equipment can be transferred from one machine to the other. In future, parametric studies of the problem on which Terzaghi made comments, "foundations on stratified soils", will obtain data with an accuracy unattainable from tests at full scale in the field; when that day comes, and centrifuge technique and observation in the field are reliable experimental mechanics, a calculation may need not to be a "crude estimate".

In the case of the jackup, the three legs apply cyclic loads of the order of ten thousand tonnes to spud cans bearing on a sea bed. When jackup spud fixity was modelled in the Cambridge 10m diameter beam and 2m diameter drum centrifuges, Dean et al (1993) studied the bearing capacity of conical footings on sand in relation to the behaviour of spudcan footings of jackups, as part of theoretical and experimental studies undertaken over a period of several years. The work as reported in publications and CUED theses (e.g. Tsukamoto PhD (1994)) tested foundation fixity of a model jackup with three independent legs, deployed at successive locations on a model "sea bed" round the wall of the 2m drum. Foundation fixity now is described by a yield locus rather than by "bearing capacity factors". The model test data are equivalent to observations of limit states in hundreds of storms offshore. The offshore industry has good experience of both beam and drum centrifuge modelling. Each year the offshore industry deploys jackups for ever longer periods in ever deeper water, and needs ever better guidance to select units that are appropriate for successive projects.

In 1929 Terzaghi made full scale tests on retaining walls, and he makes his mistrust of earth pressure theory clear in the title of a paper that he presented to the Boston Society of Civil Engineers on May 20, 1936, "A fundamental fallacy in earth pressure computations", (the only paper reprinted in full in the 1936 Proceedings). He draws attention to small ground movements that he observed and asks how forces measured in trench supports relate to strain in ground beside the trench. He complains that "the factor ‘strain’ does not enter the theory" and his first conclusion is that

"The fundamental assumptions of Rankine’s earth pressure theory are incompatible with the known relation between stress and strain in soils, including sand. Therefore the use of this theory should be discontinued".

In spite of this, Rankine’s theory is still in use 60 years later in a third edition of his text book, Terzaghi, Peck and Mesri (1996). An opportunity was missed in 1936 to see that problems with earth pressure theory are caused by an error in "Mohr’s hypothesis".

Coulomb solved by statics some problems of plane bodies for which the limiting stress criterion has a form F(s _x,t _xy,s _y)=0. Limiting plane equilibrium satisfies the two equations,

d s _x/d x+d t _xy/d y=0, d t _xy/d x+d s _y/d y=0;

the system of three equations in the three unknowns (s _x,t _xy,s _y) is of the hyperbolic type. Strain has no place in the mathematics. For a criterion F=0 of the Mohr Coulomb type, in a plane limiting stress field, there are two characteristic directions along each of which a function of the magnitude and direction of stress maintains a constant value. Stresses are defined at each point on a particular length of boundary, and in a triangular "domain of dependence" the stress at a place in the domain is fixed by values of these functions that are propagated to that place along the two characteristics that reach that place from two points on boundary. The only good reason for use of the equations to be discontinued is that one or other of the equations does not apply. The equilibrium equations are beyond question. But, from the fact that Terzaghi found that strain does affects earth pressures, he should have deduced that there is an error in the Mohr Coulomb equation; either cohesion, or friction, can not be "true" properties of soil, independent of strain conditions.

Terzaghi’s error in interpreting the data of Hvorslev’s drained shear box tests in terms of "true" cohesion and friction, is explained by Schofield (1993,1998). In over consolidated clay paste the peak strength increases because the particles become densely packed, not because of molecular attraction of "cohesive" soil particles. Critical state friction is the reliable part of clay peak strength. There is an unreliable transient part of clay peak strength due to "interlocking", Taylor (1948), which is the same as "arching". We can see from the increased water content in gouge material on slip surfaces, that stiff clay at peak strength is dilating as it shears and softens. Peak strength instability is like buckling in the sense that it involves geometry and strain boundary conditions. It is not defined uniquely in stress space, or by Mohr’s circles with a "true" curved envelope which can be fitted approximately by the Mohr Coulomb equation.

Coulomb and Rankine did not test soil in a shear box. They distinguished solid rock with strength in a tensile test, from soil whose disturbed parts do not adhere. They saw that a drained slope of soil has an angle of repose which they called the angle of friction. This was the strength parameter that they relied on in design. For the angle of repose to be a soil constant, all shear deformation down slope must be at constant volume. Soil which deforms continuously at constant volume, in a drained shear test or below a slope at repose, must be in critical states with q=Mp’. This applies equally to soil with coarse and with fine grains.

Schofield and Wroth (1968) describe liquid limit tests as undrained behaviour of soil in critical states. The apparent cohesion of test samples of fine grained soil with low permeability is equal to suction times critical state friction. It increases as effective stress increases. Soil yields in a stable manner on the wet side of critical states, at stress ratios less than critical, where q<Mp’. Plastic yielding of such soil is predicted by the cam clay theory.

A centrifuge model made of reconstituted soil paste can have zones of plastic yielding, in which very many tests of elementary volumes of soil each experience a different true triaxial test, with compression and shear strain on the wet side of critical states. A particular soil can exhibit anisotropy if it has such tendencies. The geotechnical centrifuge is a good apparatus for testing reconstituted soil on the wet side of, or near to, critical states.

Failure with q>Mp’ on the dry side of critical states involves unstable behaviour. Faulted soil dilates in shear, causing water to be sucked into slick soil paste on the failure plane. Soil will fissure at low effective stress. If there are cracks, pipes, or channels in a zone across which there is a high hydraulic gradient, rapid transmission of pore pressure into the soil will transform what was initially a stiff, lightly stressed, continuous soil body into a clastic debris flow. When this effect is seen in centrifuge model tests it is described as liquefaction. Some effects may not scale, and care is needed. Whenever it is claimed that progressive failure at homologous points in a model and a prototype are similar, the interlocking geometry, effective stress, and transient seepage flow all have to be correct within the zones through which instability propagates. This should be validated by modelling of models.

Today "a thorough grounding in theory" should include both a critique of Mohr, and also the ideas of critical state soil mechanics. The above description of the behaviour of reconstituted soil paste follows from work by Taylor at MIT, and later work in CUED. We reconstitute soil to make centrifuge models of any material that is selected for a compacted fill. We use the same technique for sites chosen for construction requiring compaction or other improvement of the ground. We understand such soils, but we need to work more on ageing, creep, and cohesive bonds, before we can make reliable models of undisturbed ground or soft rock.

The factor "strain", that Terzaghi wanted to see introduced into the theories, is present as significant plastic strain in mechanisms that we observe. Tests in which models suffer large strains disclose the three regimes of large strain behaviour, (fissure, fault, fold), that we also see at full scale. Our tests complement observational methods, with larger strains and more extensive parametric studies than are achieved in the field. Our test data are used to validate numerical models and our small scale tests have a fundamental basis. A model made of soil paste relies on a law of soil mechanics that was stated by Coulomb, reconstituted soil has no adhesion; both he and Rankine dismissed cohesion from design calculations. TC2 is both near the "centre of gravity of research" and also that of design. In critical state soil mechanics design is seen as being not so difficult if we consider the ultimate fully remoulded condition that might occur if the process of uniform distortion were carried on until the soil flowed as a frictional fluid. This limit state is achieved and studied in centrifuge tests to failure.

TC2 began with seminars in Tokyo, Manchester, Davies, and with a committee meeting after the San Fransisco Conference, following which Craig, James and Schofield published a book of invited contributions on centrifuges in soil mechanics. Subsequent TC2 committees have held workshops and conferences, leading to publications which establish the validity of many centrifuge techniques. The next committee has a duty to make a report to the Conference in 2001. We should claim a fundamental significance for centrifuge tests on models made of reconstituted soil, and explain how our tests can correct some errors that were made in Harvard. If it led to serious discussions in Istanbul, it would be good for Terzaghi’s Society.

Arulanandin and Scott (1994) editors, Proc. Int. Conf. on Verification of Numerical Procedures for the Analysis of Soil Liquefaction Problems, at U.C. Davis; Volumes 1 & 2; Balkema.

Carrak (1998), Carrak Measurement Technology, Cables Farm, Station Road, Dullingham, Newmarket, Suffolk, England, CB8 9UP, tel. 44 (1638) 507192.

Dean, James, Schofield, Tan, and Tsukamoto (1993), "The bearing capacity of conical footings on sand in relation to the behaviour of spudcan footings of jackups" pp 230-254 in Proc. Wroth Mem. Symp., edited by Houlsby and Schofield, Thomas Telford, London.

Derkx, Merliot, Garnier, and Cottineau (1998), Centrifuge 98 Vol. I, pp 97-102,

Malushitsky (1975), The centrifugal modelling of waste-heap embankments. Russian edition, Kiev, English translation edited by A. N. Schofield, Cambridge University Press (1981).

Pokrovsky and Fedorov (1936) appended; Proc. 1^st Int. Conf. ISSMFE (Harvard) Vol. I, p 70.

Schmidt (1988), in Centrifuges in soil mechanics; Craig, James and Schofield eds. Balkema.

Schofield (1993), From cam clay to centrifuge models, JSSMFE Vol. 41, No. 5 Ser. No. 424 pp 83- 87, No. 6 Ser. No. 425 pp 84-90, No. 7, Ser. No. 426 pp 71-78.

Schofield (1998), "Mohr Coulomb Error Correction", Ground Engineering, August, pp 30-32

Schofield (1998), "The Mohr Coulomb Error", in Colloque, Mécanique et Géotechnique, Jubilé Scientifique de Pierre Habib, 19 Mai 1998, LMS École Polytechnique, Paris.

Schofield and Wroth (1968), Critical State Soil Mechanics, McGraw-Hill, London.

Stewart, Boyle, and Randolph (1998), in Centrifuge 98, Vol. I, pp 35-40.

Taylor (1948), Fundamentals of soil mechanics, pp 346-7, Wiley, New York.

Terzaghi (1936); Proc. 1^st Int. Conf ISSMFE (Harvard), Vol. III, pp 13-18, 261-3.

Terzaghi, Peck and Mesri (1996), Soil Mechanics in Engineering Practice, Wiley, New York.